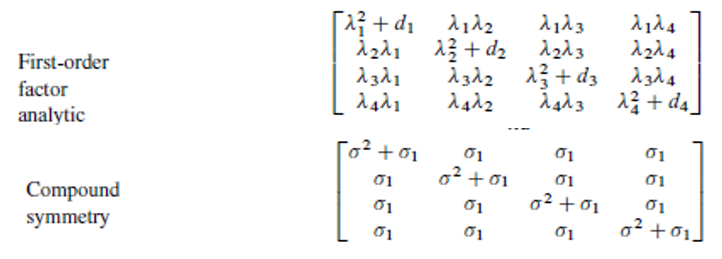ANOVA: The conventional method vs the mixed model

Abstract: In this paper, we provide a brief review of conventional ANOVA and its counterpart mixed model. We provide a comparison of the two models and briefly discuss the models recommended by the agencies.
Analysis of Variance, also known as ANOVA, is one of the most widely used statistical methods in various industries, particularly in pharmaceutical industry. In summary, the basic ANOVA model compares a continuous variable across several classes and provides a conclusion of whether there are any differences between the classes in regard to the given continuous variable.
One generalization of ANOVA called the repeated measure ANOVA allows using a second repeated factor in the model. This second factor is typically a repeated measure of the observations. Whenever such repeated measures are present in the data, another statistical analysis approach is the mixed model. This model introduces a new correlation structure to the analysis and evaluates the statistics on this basis.
In certain situations, the two models can provide very similar, sometimes identical, results while in other circumstances they can generate slightly different results. We will provide a short summary of the models and present a comparison of them.
ANOVA
ANOVA, or Analysis of Variance, is a method used to compare means of multiple groups in order to identify any statistically significant differences among them. Normally when there are only two groups of interest, and there is no other factor to be considered in the model, a t-test would suffice. However, ANOVA is commonly employed when comparing means from three or more groups or when we need to take other factors such as repeated measures into consideration.
The first step of ANOVA involves formulating null and alternative hypotheses. The ultimate goal of this hypothesis testing is to decide whether we can reject the null against the alternative.
This is done through the derived p-value. If the p-value is significant (mostly the significance level is set to .05 meaning that any p-value smaller than this would be considered significant), then the null hypothesis is rejected against the alternative hypothesis. This indicates that there is a significant difference between the means of the two groups.
This is very important, noting that a significant p-value doesn’t indicate that “all” means are significantly different. It is also worth noting that a non-significant p-value doesn’t necessarily mean that there is no difference between the means! It simply indicates that there is no evidence for a significant difference. However, it should be borne in mind that “Absence of Evidence does not mean Evidence of Absence”!
ANOVA is performed on the basis of the notion of variance, which measures the variability or spread of data within each group. Variability in the observed data has two main sources: the variance between the group means which is referred to as the “between-group variance” and the variance within each group which is referred to as the “within-group variance”.
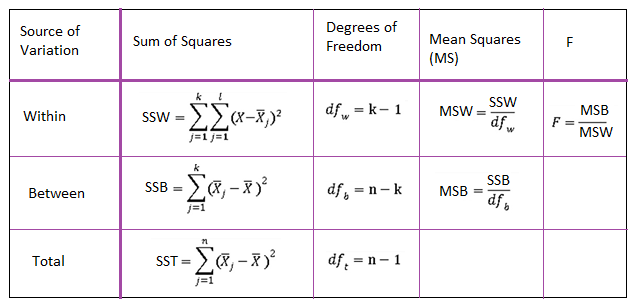
After calculating the variance, the ANOVA test statistic is calculated by normalizing the within and between variances. The test statistic associated with ANOVA is the F-Statistics. The F-statistics is calculated by dividing the variances by their degree of freedom and then calculating the corresponding ratio. The table below, known as the ANOVA table, summarizes this process.
Figure 1 – ANOVA Table
Typically, a large F-statistic is an indication of a significant difference among the group means. This is when we reject the null hypothesis against the alternative hypothesis. However, the standard measurement for such a conclusion is usually not the observed F-value, but the p-value pertinent to it. P-value depends on 3 factors: the observed F-value and the two degrees of freedom discussed above.
As specified in the preceding paragraphs, a p-value smaller than the significance level is considered significant, resulting in rejecting the null hypothesis. In most statistical inferences, including ANOVA, regression, t-statistics, etc., the significance level is set to .05. Although, in some studies, it could be set to .1 or .01.
It should be pointed out that significant conclusions based on the smaller values of significance levels are more reliable. However, there is a trade-off between the statistical power and the significance level, and that is why a significance level of .05 is more widely used in statistics.
Mixed Models
Mixed models or more precisely mixed effect models are statistical models that can substitute the conventional ANOVA. Mixed models typically have a more complex structure compared to ANOVA. An important feature of the mixed models is that they allow defining a correlation structure. This removes a flaw related to ANOVA: one of the requirements of ANOVA is that the data points should be independent. This requirement might not be met when we have multiple observations per subject.
As an example, in crossover bioequivalence studies, a subject can provide at least two data points, each from a dosed treatment. Therefore, the two observed data points are dependent through the subject. A mixed model can explain this sort of dependence in the model using the correlation structure.
When there is no correlation structure in the model, all the covariances between the observed data are set to 0. This is the case with ANOVA. With a correlation structure, some covariances are set to non-zero values. How these non-zero values are defined depends on the type of the correlation structure that is chosen. Figure 2 presents the two most commonly used structures.
In a simple language, for crossover bioequivalence studies, the First structure, also known as FA(1), assumes different variances for different treatment groups, it also assumes different covariances between different pairs of treatment groups. The second structure, also known as CS, assumes the same variance for different treatment groups and the same covariances between different pairs of treatment groups.
FA(1) introduces a more complex model than CS, as it uses more parameters. As to which correlation structure to use could be answered by the rule of simplicity, as discussed in the next section.
Figure 2 – Two commonly used correlation structures
This is important to note that the conventional ANOVA model works through constructing the ANOVA table, where the within and between subject variabilities are separated and the F statistic is constructed. The mixed model doesn’t employ such a structure. Instead, it deploys the usual structure of linear models, which is based on estimating the parameters for all the factors in the model. ANOVA is simulated through such a structure.
Which Model to Use; ANOVA or Mixed Model?
In statistics, there is a general rule called the rule of simplicity. The rule says if a couple of models fit the data nearly equally good, it is always preferable to use the simplest model. The reason is that complexity comes at the cost of more parameters to estimate. This can cause issues such as overfitting or lack of convergence.
Overfitting means that the model fits the observed data so well that it is unlikely to represent unobserved data! Lack of convergence means that the required parameters in the model cannot be estimated. From this perspective, if we believe that there is no dependence in the data or the dependence is negligible, then we had better use ANOVA instead of mixed model.
That said, mixed models still have a nice feature that makes them more suitable in some situations compared to ANOVA: Mixed models can handle unbalanced and missing data better. While ANOVA can entirely remove the unbalanced data, a mixed model can still allow them to contribute to the analysis.
Mixed models have another advantage over ANOVA that doesn’t typically apply to clinical trial studies (at least not to bioequivalence studies and Phase 1 clinical studies). However, this could still be an important factor in other fields. Basically, ANOVA has not been designed to play continuous covariates! This means that in ANOVA, all the covariates are considered categorical. For instance, subject, sequence, period, and treatment are the most frequently used categorical covariates in bioequivalence studies.
On the other hand, as a more general model, mixed models allow a mixture of continuous and categorical covariates. This is, as an example, important in clinical and bioequivalence studies where time is a crucial factor. In such studies, if one uses ANOVA, time has to be treated as a categorical covariate while in most cases it makes a far better sense to treat time as a continuous covariate. This could be easily handled using a mixed model.
ANOVA and Mixed Models in Bioequivalence Studies and Agencies Approach Towards Them
As explained above, ANOVA and mixed models have their pros and cons. As a result, there is no consensus on which model to use to analyze the bioequivalence study data. However, based on tons of studies performed, it is almost accepted that for two-way crossover studies, the results from the two models are often very similar and sometimes identical. Therefore, the conventional ANOVA is preferable as it is simpler.
Even so, still some sponsors prefer to have such studies analyzed using the mixed model. One reason could be the mixed model’s ability in handling the missing and unbalanced data.
Crossover studies for EMA are analyzed using ANOVA while FDA studies could be analyzed using either of the two models, although ANOVA is by far the more common model.
For fully replicate studies, the mixed model could possibly do a better job. The situation here is not as simple as it is with the two-way crossover studies. Basically, multiple observations per subject per treatment could result in more correlated (dependent) data that could make mixed models more suitable. FDA requires analyzing such studies using a mixed model, while EMA recommends using ANOVA.
It is worth noting that the mixed model used for fully replicate designs for FDA submissions are not directly applied to the observed data. The data is first processed by evaluating the differences between the observed data for each subject and for each treatment. The mixed model is then applied to these differences to both calculate the intra-subject variability and the ratio, as well as the confidence intervals for the geometric means.
Partial replicate studies for EMA are analyzed using ANOVA. For FDA, a similar approach as that for the fully replicate designs is used. However, instead of a mixed model, a GLM model is used.
ANOVA and Mixed Models; Final Thoughts
The choice between conventional ANOVA (Analysis of Variance) and mixed models is dependent on the specific context and requirements of the study. Both have their advantages and disadvantages, with ANOVA being the more straightforward method but mixed models offering increased flexibility and the ability to define a correlation structure, making them particularly suitable for handling repeated measures and multi-level data.
In general, the ‘rule of simplicity’ in statistics suggests choosing the simplest model if multiple models fit the data adequately. This means ANOVA would typically be preferred if there’s no substantial data dependence or if such dependence is negligible. However, mixed models have demonstrated superiority in certain scenarios, such as dealing with unbalanced or missing data, and accommodating continuous covariates, which ANOVA treats as categorical. Researchers need to consider the nature and requirements of their data, the simplicity of the model, and any potential guidelines from regulatory agencies when choosing between ANOVA and mixed models.
Why Choose BioPharma Services?
For drug development sponsors, the assistance of a CRO such as BioPharma Services can be invaluable in navigating these decisions. With an expert team of statisticians understanding of both ANOVA and mixed models, BioPharma Services can guide sponsors in selecting the most appropriate statistical method for their studies based on the design of the study, the nature of the data, and regulatory guidelines.
BioPharma Services provides comprehensive services, covering everything from early-phase drug development through to post-approval activities. Our team is well-versed in various therapeutic areas and regulatory requirements, ensuring sponsors receive not only expert statistical analysis but also guidance on study design, clincial trial data management, regulatory submissions, and overall project management. Therefore, in terms of selecting between ANOVA and mixed models for Bioequivalence Studies or any other drug development processes, BioPharma Services offers the knowledge, experience, and versatility to support sponsors in making the best decisions for their projects.
Written by: Jafar Soltani Farsani
BioPharma Services, Inc., a Think Research Corporation and clinical trial services company, is a full-service Contract Clinical Research Organization (CRO) based in Toronto, Canada, specializing in Phase 1 clinical trials 1/2a and Bioequivalence clinical trials for international pharmaceutical companies worldwide. BioPharma has clinical facilities both in the USA and Canada with access to healthy volunteers and special populations.